The Metastatistical Extreme Value Distribution

Density, distribution function, quantile function and random generation for the MEV distribution with shape parameter 'w', scale parameter 'c'. Parameter 'n' refers either to the mean number of wet days per year in case of the simplified MEV, or to the number of wet days for each year.

Usage

dmev(x, w, c, n)

pmev(q, w, c, n)

qmev(p, w, c, n)

rmev(N, w, c, n)

Arguments

x, q: numeric vector or single values of quantiles for dmev and pmev.
w, c: vector or single values of shape and scale parameter of the MEV distribution. If a vector, w and c must have the same length as n.
n: Either mean number of wet events per year for the SMEV, or a vector for yearly MEVD calculations, i.e. one value per year (see details). If a vector, n must have the same length as w and c.
p: vector or single value of probabilities for qmev.
N: Number of observations to sample from the MEVD or SMEV.

Value

dmev gives the density function, pmev gives the distribution function, qmev gives the quantile function and rmev provides random realizations of the SMEV and MEVD.

Functions

pmev(): distribution quantile function
qmev(): quantile function
rmev(): random generation function

Examples

# SMEV
dmev(1200:1300, 0.7, 20, 110)
#>   [1] 2.646170e-08 2.618540e-08 2.591207e-08 2.564165e-08 2.537413e-08
#>   [6] 2.510947e-08 2.484764e-08 2.458860e-08 2.433233e-08 2.407880e-08
#>  [11] 2.382798e-08 2.357983e-08 2.333434e-08 2.309146e-08 2.285117e-08
#>  [16] 2.261344e-08 2.237825e-08 2.214556e-08 2.191536e-08 2.168760e-08
#>  [21] 2.146227e-08 2.123934e-08 2.101878e-08 2.080057e-08 2.058468e-08
#>  [26] 2.037108e-08 2.015976e-08 1.995068e-08 1.974382e-08 1.953916e-08
#>  [31] 1.933667e-08 1.913634e-08 1.893812e-08 1.874202e-08 1.854799e-08
#>  [36] 1.835602e-08 1.816608e-08 1.797816e-08 1.779223e-08 1.760827e-08
#>  [41] 1.742626e-08 1.724618e-08 1.706800e-08 1.689170e-08 1.671727e-08
#>  [46] 1.654469e-08 1.637393e-08 1.620498e-08 1.603781e-08 1.587241e-08
#>  [51] 1.570875e-08 1.554683e-08 1.538661e-08 1.522808e-08 1.507123e-08
#>  [56] 1.491603e-08 1.476247e-08 1.461052e-08 1.446018e-08 1.431142e-08
#>  [61] 1.416423e-08 1.401859e-08 1.387449e-08 1.373190e-08 1.359081e-08
#>  [66] 1.345120e-08 1.331307e-08 1.317638e-08 1.304113e-08 1.290731e-08
#>  [71] 1.277489e-08 1.264386e-08 1.251421e-08 1.238591e-08 1.225897e-08
#>  [76] 1.213336e-08 1.200906e-08 1.188607e-08 1.176437e-08 1.164394e-08
#>  [81] 1.152478e-08 1.140686e-08 1.129018e-08 1.117472e-08 1.106047e-08
#>  [86] 1.094742e-08 1.083555e-08 1.072484e-08 1.061530e-08 1.050690e-08
#>  [91] 1.039964e-08 1.029349e-08 1.018846e-08 1.008452e-08 9.981668e-09
#>  [96] 9.879889e-09 9.779172e-09 9.679506e-09 9.580880e-09 9.483282e-09
#> [101] 9.386702e-09
pmev(1200:1300, 0.7, 70, 110)
#>   [1] 0.9289803 0.9292715 0.9295616 0.9298504 0.9301380 0.9304244 0.9307096
#>   [8] 0.9309937 0.9312765 0.9315581 0.9318386 0.9321179 0.9323960 0.9326729
#>  [15] 0.9329487 0.9332233 0.9334968 0.9337691 0.9340403 0.9343103 0.9345792
#>  [22] 0.9348470 0.9351137 0.9353792 0.9356437 0.9359070 0.9361692 0.9364303
#>  [29] 0.9366903 0.9369492 0.9372071 0.9374638 0.9377195 0.9379741 0.9382277
#>  [36] 0.9384801 0.9387316 0.9389819 0.9392312 0.9394795 0.9397267 0.9399729
#>  [43] 0.9402181 0.9404622 0.9407053 0.9409474 0.9411885 0.9414285 0.9416676
#>  [50] 0.9419056 0.9421427 0.9423787 0.9426138 0.9428479 0.9430810 0.9433131
#>  [57] 0.9435442 0.9437744 0.9440036 0.9442319 0.9444592 0.9446855 0.9449109
#>  [64] 0.9451354 0.9453589 0.9455814 0.9458031 0.9460238 0.9462436 0.9464624
#>  [71] 0.9466804 0.9468974 0.9471135 0.9473287 0.9475430 0.9477565 0.9479690
#>  [78] 0.9481806 0.9483913 0.9486012 0.9488102 0.9490183 0.9492255 0.9494319
#>  [85] 0.9496374 0.9498420 0.9500458 0.9502487 0.9504508 0.9506521 0.9508524
#>  [92] 0.9510520 0.9512507 0.9514486 0.9516456 0.9518419 0.9520373 0.9522319
#>  [99] 0.9524256 0.9526186 0.9528108
qmev(1 - 1 / seq(5,50,5), 0.7, 70, 110)
#>  [1]  948.9202 1116.9967 1215.4018 1285.7748 1340.7865 1386.0482 1424.5527
#>  [8] 1458.0898 1487.8169 1514.5267

# MEVD: 50-year event of 10 years Weibull series
w <- rnorm(10, 0.8, 0.1) # shape parameter
c <- rnorm(10, 200, 30) # scale parameter
n <- rnorm(10, 200, 50) # number of wet days
qmev(1 - 1 / 50, w, c, n)
#> [1] 4917.247

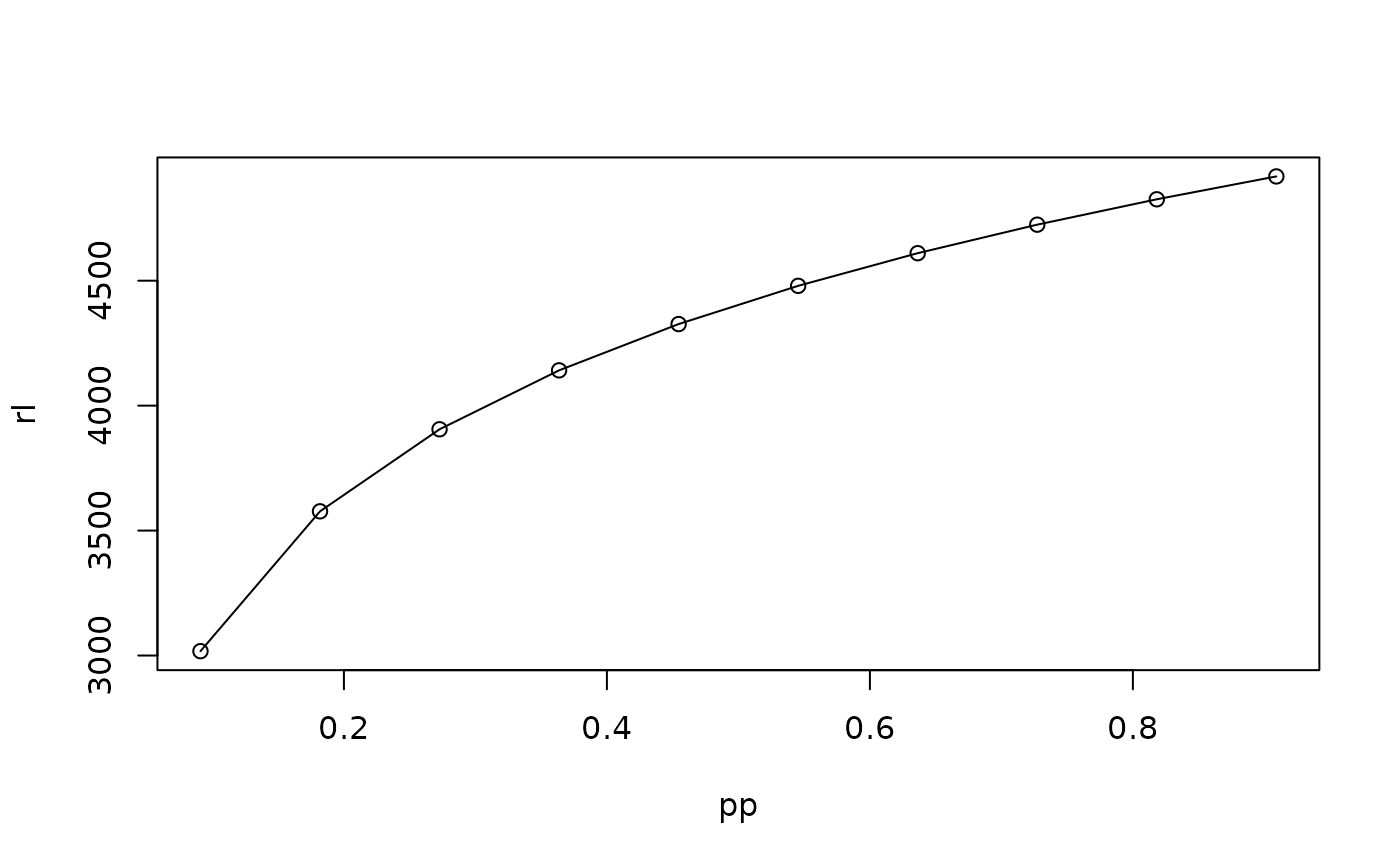
# rl-plot
rp <- seq(5, 50, 5)
rl <- qmev(1 - 1 / rp, w, c, n)
pp <- (1:length(rp)) / (length(rp) + 1)
plot(pp, rl, type = "o")